计算机的运算方式

无符号数和有符号数

无符号数

寄存器的位数反映了无符号数的表示范围

例如8位就表示0～255，16位表示了0～65535

有符号数

真值就是带符号的数，而机器数就是将符号数字化了的数 0正 1负

机器数分为：

• 原码
• 补码
• 反码
• 移码

原码

原码的n位定点整数表示范围是：$-(2^{n-1}-1 )$~$+(2^{n-1}-1)$

原码表示的n位定点小数的表示范围是：$-(1-2^{-(n-1)})$~$+(1-2^{-(n-1)})$

补码

作用是化减法为加法

以时钟12进制为例子，+9是-3以12为模的补数

一个负数加上“模”即该负数的补数

当一个正数和一个负数互为补数时，他们绝对值之和为模数

正数的补即为本身

负数的补加模n即可 一般二进制的话模的就是$2^{n+1}$ (这里假设是n位整数了)

当真值为负，补码可以用原码除符号位外每位取反，末位+1得到

补码的n位定点整数表示范围是$-2^{n-1}$~$+(2^{n-1}-1)$

补码表示的n位定点小数的表示范围是 $-1$~$+(1-2^{-(n-1)})$

反码

移码

用来弥补补码难判断真值大小的问题

补码和移码只相差一个符号位

用移码能表示浮点数的阶码，能方便判断浮点数阶码的大小

数的定点表示和浮点表示

定点表示

小数点按约定方式标出

浮点表示

$N=S \times r^j $

浮点数的一般形式，其中S是尾数、j是阶码、r是基数

r一般取2，4，6，8

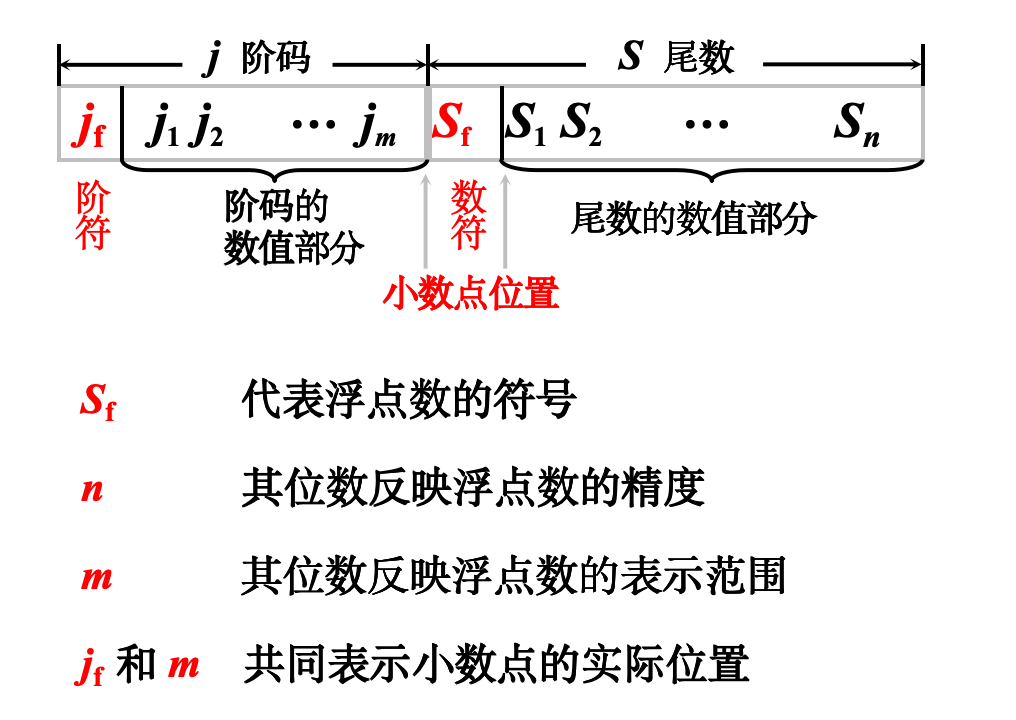
规格化形式：尾数绝对值的最高位（第一位）必须为1，即尾数的绝对值必须大于或等于1/R，这样浮点就有n个有效数字

基数r越大，可表示的浮点数范围越大，精度降低

定点运算

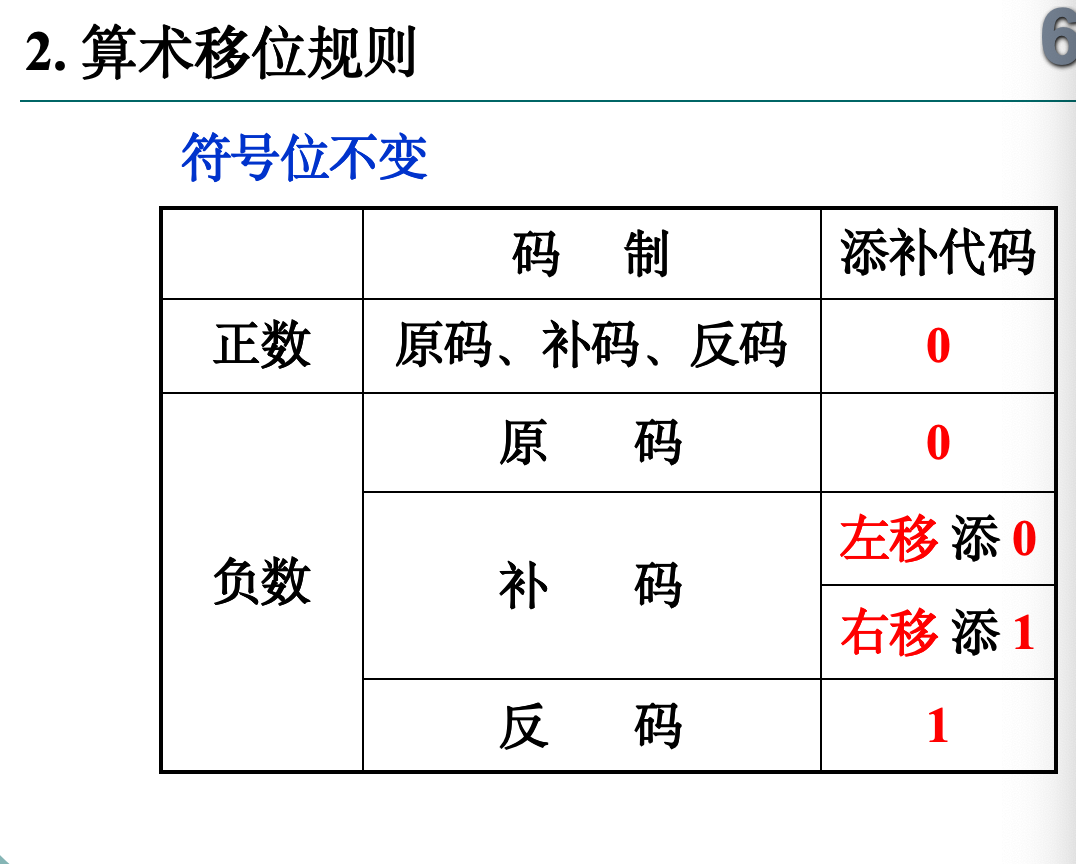
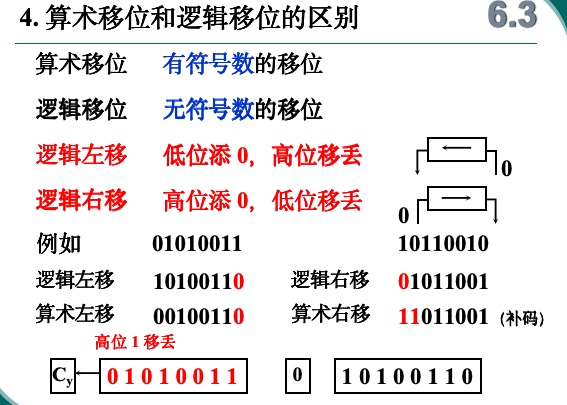
移位运算

移位和加减配合能够实现乘除法

加减法

加法有

$$整数：&[A]_补+[B]_补 = [A+B]_补 mod\space 2^{n+1} \\ 小数：&[A]_补+[B]_补 = [A+B]_补 mod\space 2^n$$

减法有

$$整数：&[A-B]_补 = [A+(-B)]_补 = [A]_补+[-B]_补 \space mod \space 2^{n+1}\\ 小数：&[A-B]_补 = [A+(-B)]_补 = [A]_补+[-B]_补 \space mod \space 2^{n}$$

连同符号位一起相加，符号位的进位自然丢掉

会存在溢出，当运算结果超过了机器数范围就会溢出